Design And Topology Of An Algorithm
Can we automate the generation of algorithms? Can we devise a technique to discover new ones? I intend to define a search space to find an algorithm, verify its presence, and find it, as opposed to analysing known ones.1 My aim primarily is to enable an experience of abstract reasoning and the joy of algorithm discovery. Before plunging into the machinery that enables us to discover an algorithm, let us meditate for a moment on the universality of inventiveness: the general process of thought science seems to hold irrespective of one's domain of specialization. This post is the first of many under the series of composing a technique to automatically discover new algorithms.
Say you got a chance to closely but unobtrusively observe your favourite brilliant scientist. As he goes about finding an elegant solution for a new problem, a lot of exploration happens. They study the literature, by looking at existing techniques and numerous variations, from their field and/or any other relevant fields. They concoct new combinations of known techniques or variations, failing at many and succeeding at few, and starting exploration on those pieces all over again.
The design of algorithms began as art. And even today, most people learn only by watching others perform. Such learning or exploration more often than not involves learning new techniques, making corrections, and conjectures what techniques could be sub-steps in the desired overall solution. A lot of thought exercises and trial-and-error experimentation goes into it. They would be helped in this exploration by an unwavering focus on the goal, an uncommonly precious common sense, incisive thought and insight, his energy, intensity, and uncompromising zeal to find the best possible (optimal) solution.
There seems to be something universal about advanced scientific problem solving by intelligent humans, even though their needs, interests, and training may be worlds apart. Fascinated by this observation, I asked myself this question— Can we build an AI system to mimic this complex process, autonomously, and discover new solutions that are useful and intelligent, if not downright brilliant?
If we can indeed build such a capable intelligent system, it would beat the best human scientists in at least three ways:
- Area Agnostic -- the same system can solve complex problems from literally any field;
- Blazingly Brisk -- its process of scientific discovery is likely to be orders of magnitude faster than that observed in brilliant humans; and
- Cognitively Consistent -- its power to ponder and discover would be constantly on and full, unaffected by moods, emotions, fears of failure, etc.
The Melting Pot
A brilliant scientist is good at understanding the field better. He breaks the complexities of the subject into various simplexities. And if he can recall all of those disassociated simplexities, he gets an understanding of the big picture. This process requires the aspect of understanding.2
Consider for example, the number 8. A scientist can count upto eight, knows what eight is, compute on it and infer its relationships with other observations— but he cannot comprehend all of this at once. This sets the theoretical limit for our scientist. Our system can surpass thus limit by collective comprehension abilities and datum-analysis separation. The goal is to augment to the science of non-understanding as opposed to understanding, by not necessarily understanding the complexities.
The system need not understand the domain, need not extract features from data, and may not even need to look at the data. It does not simply do an efficient but blind search through an enormous hypothesis space. In short, it does not look in the space of all possible explanation for the observed data, like, say, a deep learning network would.
The system is guaranteed to be more efficient than today's deep learning methods and rapidly searches through a much smaller, much better organised, space of plausible new algorithms that custom-fit the given data. These combinatorial algorithms (counting, permuting, etc.) can then be applied to the data to find patterns, to build a model, etc. Until this last step, it is possible that it would not even need to see the data. Its domain of play is the melting pot of the collective and connected thoughts of dozens or perhaps hundreds of human scientists. It is in this melting pot that techniques keep taking birth, evolving, morphing, combining and disintegrating.
I do not intend to propose a fully contained self-referential system. I am mindful of the impossibility of reducing the I/O processing of human mind to a complex algorithm. This forms a theoretical limit on the nature of discoverable algorithms. That is to say, the system can never come up with an algorithm on its own that can discover fundamental truths about algorithms.
Nothing can be decided about computability of my technique and the algorithms discoverable by it. Same can be said about automatic reasoning of algorithms.
Representation
An abstract entity performing a transformational process in the computing world, is called an algorithm. Its precise representation in a computer readable formalism is called a program, which can be in any programming language.
The problem that an algorithm is set to solve is specified by two components:
- A precise definition of set of legal input
- A precise characterisation of desired output as function of input
We regard input and output sets as data and an algorithm as a set of instructions operating on them. Many real-world algorithmic problems are not easy to define. Consider for example the problem of weather prediction, evaluation of stock market investments, etc., requiring hard to specify inputs or outputs.
Technical studies of algorithms are mostly concerned with verification (proof of correctness) of a given algorithm or with examining its characteristics (computational complexities) as a computational tool. Such mathematical studies tell us little about how the algorithm was developed in the first place. Let us consider a small example involving sorting and searching algorithms. Take the bubble sort algorithm proposed by Donald Knuth in his famous book The Art of Computer Programming.
This algorithm operating on n items has a running time proportional to n^2, which grows very fast in practice. The excitement around algorithms grew when people began to design faster sorting algorithms like quick sort, shell sort, merge sort, radix sort, heap sort, etc. The programs implementing these algorithms were supplemented by informal proofs of correctness by mathematical induction based on properties of natural numbers. More clever methods were developed like operating on the pointers to data, instead of moving data themselves. These involved various combinatoric techniques.
Such techniques emerged from the need to make programs run faster. We aim to tackle a few combinatorial problems from a different perspective, by building algorithms from first principles using techniques from algebraic topology, generalisation theory, formulaic manipulation and reasoning about function value changes.
In a wide-ranging treatment unusually attuned to the competing ideas of algorithmic science, responsiveness of mathematical exploration to interesting facts about algorithms is shown. I concern myself with developing algorithms from first principles, departing from standard approach of analysis and application of known ones.
Algorithmic Chemistry
Walter Fontana, in a 1991 paper, reported a novel approach to evolution of emergent phenomena. The effort failed to produce complex structures of any particular interest, albeit being able to produce simple self-organising phenomena. The approach was to let small LISP algorithms act on each other to produce new LISP algorithms. These are again added back to the primordial LISP algorithm melting pot. It was similar to a chemical system.
The simulations were carried at a large scale over long durations, yet they failed to yield anything dramatic. Many variants of the style followed suit at the time. These involved various biological, physical and chemical inspired stochastic replacement rules to prune uninteresting algorithms. None succeeded in producing complex structures. To achieve a variety of layered and complex algorithm networks, AI tools like Tensor factorisation, hyper graph mining and probabilistic logic can be jointed to Fontana's approach.
Each variety of melting pot would hold a lattice of self-organising program networks carrying desired functionality. Each set of algorithm networks collectively transform inputs to outputs as desired by an AI goal system. This can be seen as a type of probabilistic model-building genetic algorithm acting on an algorithm chemical network. The rich combinatorial potential of these networks either lend to complex emergent phenomenon or a complete non-inferential digital mess.
Factors like stability of reaction networks matter as much as the programming language underlying the algorithms (right from machine language to assembly language to high level language). The pots can be compartmentalised for parallel processing. Each LISP algorithm (with its constituent expressions and datum) is seen as a molecule (atom) with associated mass and novelty score.
Novelty score of a molecule (atom) is the distance between data flow paths within itself and a standard known algorithmic technique for a given problem. For example, consider a set of integers from 2 to N and each element of this set as a molecule in a melting pot. For a reaction rule where every molecule kills a multiple of itself, we end up with all primes between 2 and N. The novelty of this phenomenon is compared with other discovered/known techniques in terms of data flow pathways to obtain a novelty score. This score of a network is assigned to its constituent algorithms. Evolution of novelty is modelled using a sparse vector with an entry for each constituent algorithm. Useful interaction information of a series of these vectors is obtained using information theoretic measures.
Learning of this evolution leads us to the duality of searchability and decidability — is the desired algorithm present in the melting pot (decidability); and find the desired algorithm in the melting pot. With SMT-based search methods, both questions become essentially the same.
Given an oracle that answers decidability questions, efficient search for desired algorithm can be carried using SMT-solvers. With concurrent dynamics in our melting pots, we ask another related question: can the oracle be queried concurrently? If the algorithm is present in the pot, we can randomly reduce the SMT-based search to several satisfiability formulas, one of which is a probable solution.
Using hardness assumptions, randomness is eliminated and one of the SMT formulas is likely to have a solution that is also a solution to the original problem. Let us briefly look at the aspect of introduction, removal and movement of algorithms within the compartments of pots. The usefulness and coherence of algorithms are highly contextual. For example, algorithm A acts as a catalyst in a reaction, where B and C react to make D. D then reacts with B to make more C and B.
A direct mechanism can cause a cyclic reaction of multiplicities greater than two. It can simply result in a chain reaction too. With the scale of combinatorics involved in these reaction networks, it is entirely not clear on how to snip a pool of algorithms — with their ever growing overlapping and/or disjoint networks. One fundamental aspect missing from these reaction networks is structure. In other words, the melting pot is well stirred. The molecules are always populations and large numbers are needed for predictability. My primary intent is to draw attention to atoms and molecules and ascribe a mathematical structure to them. The idea is atoms of algorithms — data and instructions combine into molecules of algorithms — a control structure. We call molecules as configurations and atoms as generators. Representative classes of such generators form standard bases. Each standard base denotes the instructional and data set for a desired algorithm.
Intuition
I provide a motivation for preparing a way of building a specialised language in which an algorithm is anticipated to be easily expressible. I then offer a formulation of a universal program, in that language, that can build itself. We resort to tools offered by algebraic topology to search for a component of the universal program that solves a given problem. We can then transform it into computational program from its algebraic form. This approach is jointed by an abstract notion of the geometry of algorithms. I will expand on this later in the series, in another posts post.
To make algorithms quickly and directly, instead of by proxy, we depart from the approach of inventing ways to construct unobservable configurations using algorithmic chemical reactions. Using algebraic topology, we look at the aspects of:
- How are instructions and data connected into an algorithm?
- What can happen to such connections?
I then build a framework for algorithm discovery by answering both aspects of inquiry. This will show how general algorithm development fits into algebraic topological scheme of things, deriving some algorithms in the process. The decidability aspect of algorithm existence once established, the searchability is reduced to an optimisation problem. Depending upon its formulation, be it cost function, energy or metric minimisation, we draw correspondence to topology theory. The idea is to form an analogous graded mapping where consecutive maps annihilate each other — i.e., the boundary of a simplex (n-dimensional triangle) does not itself have a boundary. Thus, searchability is looked as equivalent to mapping something to zero.
Consider a collection of algorithms in the melting pot. Each algorithm in turn is sub-divided into a collection of sub-algorithms. The properties of sub-algorithms can be inferred based on the incidence (connectedness) relations among them. Each sub algorithm is considered irreducible and called an instruction. The whole algorithm is then represented by a collection of instructions and input data.
Think of an algorithm A. Each instruction in A has many properties (sub functionality, complexity, operators, order of its operands, etc.). To bring about a notion of equality among instructions, we say each instruction depends on and produces other instructions, which are said to be connected/incident to it. These collections of instructions that are connected to one instruction form a boundary of the said instruction.
In short, we find all instructions are equal in a sense that they all have incidence relations among them. These incidences define a boundary for each instruction. The idea is further extended to the space of all algorithms with incidences and boundaries described among them. It is important to note that the input/output elements, unlike instructions, of an algorithm have no elements incident to them. This means the boundary for data elements is absent.
Consider the collection of algorithms in the melting pot. Assuming we have a notion of a geometry of an algorithm, that is, say we can in a topographical sense, map the shape of an algorithm. We can define an equivalence relation on the collection of algorithms based on this geometry property. That is, two algorithms are called 'equal' if they yield the same geometry or shape, according to a given definition.
Let us assume this relation partitions the collection of algorithms into four sub-collections. We call the collection of four sub-collections a quotient collection. This notion of quotient collection and equivalence relation can be reduced to within a collection of instructions. Let us take a short detour to define a few concepts to help us investigate connectedness of data and instructions.
Algebraic Topology
Let me provide a minimal list of definitions and results from abstract algebra that may prove useful in our further discussion of algorithm discovery. These concepts helped me in organising my thoughts better with regard to investigating aspects of algorithms.3
A topology in a collection A is a family T of sub-collections such that their union and intersection also belong to T. We call a collection topological space whenever it has some topology defined on it. The above topological space is denoted as (A, T).
A collection of elements with well-defined associative binary operation (like addition, multiplication, etc.) with identity and inverses is called a group. It is called an additive group when it is also commutative. The torsion part of an additive group G is a sub-group of its elements g in G such that g^n = 1 for some natural number n.
A group of particular interest is Z, the group of integers. The addition or subtraction of two integers gets us another integer. We say that Z is an additive group. In certain situations, we regard two integers which differ by a fixed prime number p to be equal. We write Z_p for the collection of such integers. The addition and subtraction operations are carried in accordance to Z_p. We call Z_p a cyclic group, with order p. A famous theorem says that a finite additive group is direct sum of finitely many copies of the cyclic group Z and groups Z_p. Elements with possible repeated application on themselves and each other when produce all elements in the group, are called generators. Cyclic groups can be generated as powers of a single generator.
I sometimes forget all the mathematical definitions in details. Many have been dealt with better elsewhere. I just write them here just to remind myself the ideas behind them. For the sake of gaining a better perspective, here is a categorical representation of entities
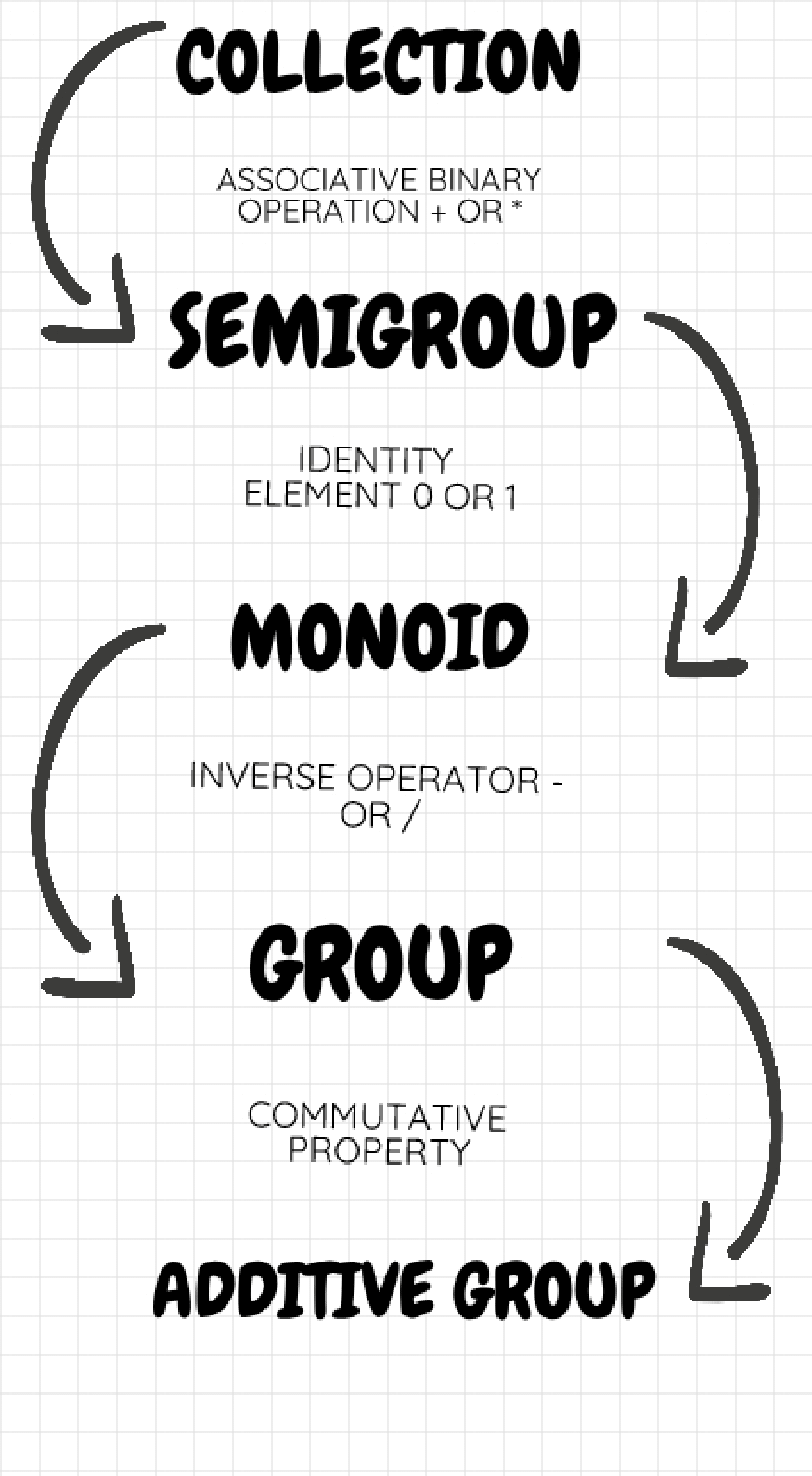
A collection is conventionally called a set. And the following definitions are written in terms of additive groups. For multiplicative groups, group addition must be replaced by multiplication, inversion by division and unity by one.
A semigroup is a set G together with an associative binary operation:
That is, for any x, y, z belonging to G,
A monoid is a semigroup with an identity e, such that for any x belonging to G,
A group is a monoid such that for any x belonging to G, there exists an inverse '-x' such that:
An additive group, also called an abelian group, is a commutative group. That is, for x, y belonging to group G,
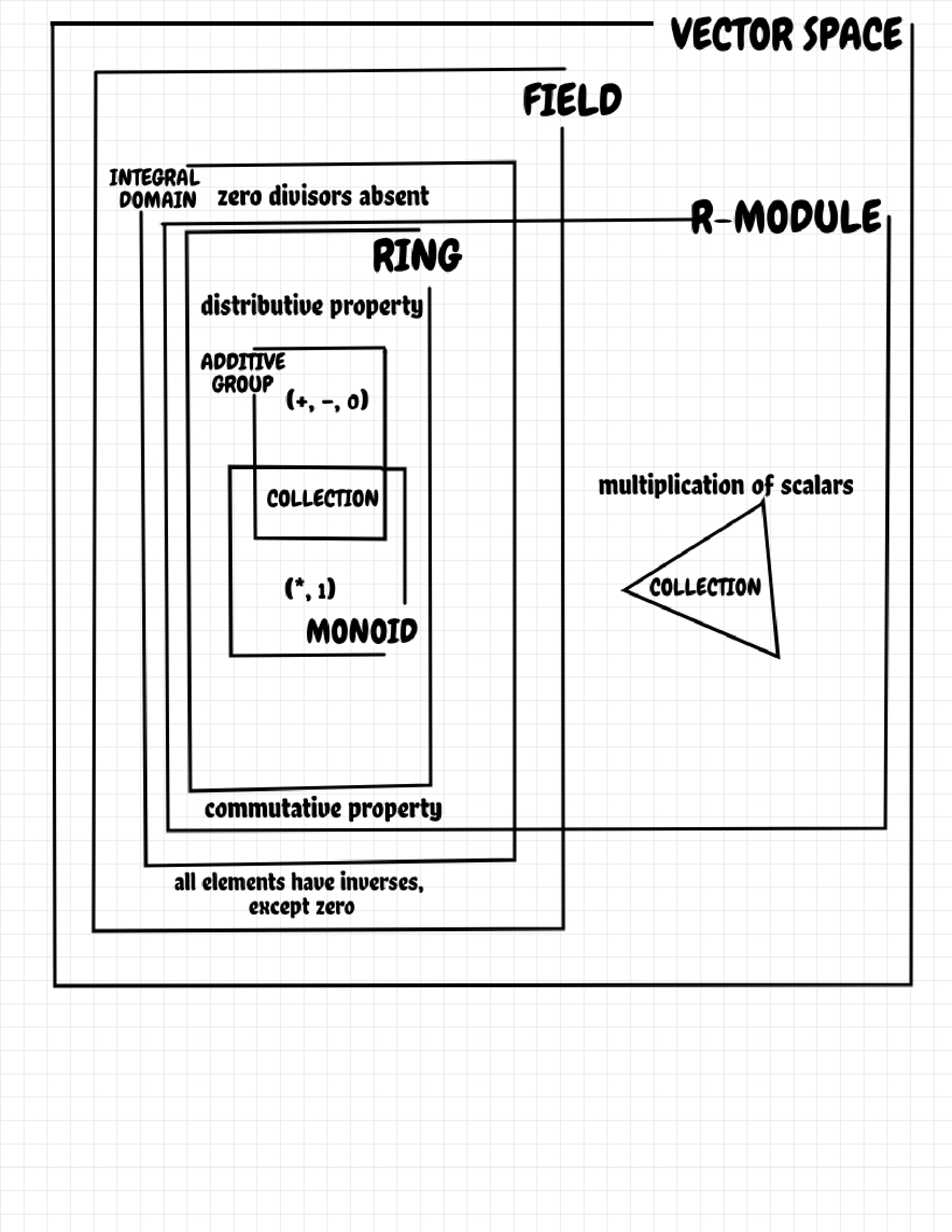
The set of integers under addition is an abelian group. The set of real numbers under addition and multiplication is also an abelian group. A subgroup is a sub collection preserving the group operation. A ring is a collection together with two identities (1, 0) corresponding to two binary operations (*, +), such that the collection is an additive group under addition and a monoid under multiplication and are bound by law of distributivity:
For example, the set of real numbers under addition and multiplication is a ring. An integral domain is a ring which is commutative under multiplication with no zero divisors. That is, no part x, y exists such that xy = 0, where 0 is the identity element under addition.
A field is an integral domain such that every element has a multiplicative inverse, except zero. A [left] vector space X over a field K is a collection X and a scalar multiplication map such that:
is bounded by usual laws of distributivity, etc. An R-module is generalisation of a K-vector space where the field is replaced by ring. An R-module is finitely generated if and only if there exists a finite set of generators or basis, and is called a free R-module if this basis is unique. Hence, a free R-module is same as a vector space. Collections, groups, rings and modules, etc. are known collectively as categories.
Consider two groups G and H, with operations + and * respectively. A continuous mapping from G to H is called a homomorphism if upon interchanging * and +, we still retain their aspects we care about. For example, let R be group of real numbers with operation 'addition'. Let us denote it by (R, +) Another group of real numbers with operation 'multiplication' be denoted by (R, *). A mapping φ defined as φ = e^x, is a homomorphism from (R, +) to (R, *). For, it can be verified that for any two real numbers a and b:
The same can be extended to topological spaces. Think of letters W, Z, X, I, N and M as topological spaces. Consider three mappings between them:
Network terminology equivalent to a few topological names are showcased in table below:
| Topological Name | Network Name |
|---|---|
| 0-cell | Point |
| 0-cycle | Pair of points |
| Basis of 0-dim. non cycles | Independent points |
| 1-cell | Branch |
| 1-cycle or boundary | Loop |
| 2-cell | Mesh |
| Basis of 2-dim. non cycles | Independent meshes |
Notions of n-dimensional round holes and n-dimensional rooms (cavities) of cell complexes can be described by their nth homotopy and nth homology groups. Imagine standing on an island and throwing a lasso flat on the ground. If there is pool of water (hole) in the island, the lasso will smoothly converge to a point as you start shrinking it. Assuming there is a pool of water on the island (and you are outside the pool), you cannot shrink the lasso to a point without getting it wet.
The fundamental group (1st homotopy group) of the island measures the degree of possibility and shrinking the lasso to a point. The 2nd homotopy group of the island measures the degree to which one can shrink a large piece of cloth to a point while always keeping the cloth on the island.
Homology attributes a family of homology groups to a topological space. Homology theories are not unique. Any additive group can be the 0th homological group of a point space pnt. For an arbitrary additive group there exists a homology. For the additive group of integers Z, its homology group is a direct sum of a finite copies of Z and Z_p, for some prime number p. One basic property of the homology groups of an n-dimensional cell complex is they vanish on dimensions higher than n and lower than 0.
Let X be an n-dimensional cell complex. We denote by k_p the number of p-skeletons of X. Its p-chain group is the direct sum of k_q copies of additive integer group Z. A chain complex of X is a long sequence of its chain groups and homomorphisms (δ_p). The homomorphisms are also called boundary operators. A basic property of chain complexes is that the kernel of pth boundary operator is a part of the image of (p+1)th boundary operator. In other words, consecutive pairs of homomorphisms annihilate each other: δ_p-1δ_p = 0. With a slight abuse of notation, it is expressed as: δ^2 = 0.
The homology of a cell complex is same as the homology of its chain complex. The homology of a chain complex is a direct sum of its pth homology groups. The pth homology group of a chain complex is the quotient group of subgroup of p-cycles by a subgroup of p-boundaries. The p-cycles are pth chains which are mapped to 0 by the boundary operator. The p-boundaries are the image of the (p+1)th chains of the boundary operator.
Each generator of a pth homology group describes a p-dimensional "hole" in the topological space. In lower dimensions, these holes can be described intuitively as connected components (dimension 0), tunnels (dimension 1), and voids (dimension 2). A higher dimensional hole may be considered a part of a topological space where a p-dimensional sphere can be attached.
The algebraic rank of a pth homology group is known as the pth Betti number b_p. Betti numbers are commonly used to distinguish different topological spaces (chain complexes) from each other. For example, a 2-sphere has a single connected component, no tunnels, and encloses a void in 3-dimensions. Its Betti numbers are thus b_0=1, b_1=0, b_2=1 (the remaining b_q are zero). In contrast, a doughnut has a single connected component, two loops (namely, one around its centre, the other around its hollow tube), and encloses a void in 3- dimensions. Its Betti numbers thus are b_0=1, b_1=2, b_2=1 (again, the remaining b_q are zero). Betti numbers can thus discern a sphere and a doughnut from each other without requiring any geometrical information about the space. This signature property of Betti numbers also applies to higher dimensions, where distinguishing different spaces from other by purely geometrical means might not be possible.
Turning our attention to the problem of computation of homology groups of cell complexes. The homology groups of a space characterise the number and type of holes in that space and therefore give a fundamental description of its structure. This type of information is used, for example, in understanding the structure of attractors from embedded time series data, or for determining similarities between proteins in molecular biology. The algebra involved in such computation depends on the nature of the coefficient group. And we will confine our discussion to the group of integers Z.
Suppose k is a cell complex. Let a group G_p(K) be generated by generators c_1^p, c_2^p, c_3^p, ..., c_k^p. Making a linear change of basis for each G_p(K), we can represent the action of the boundary operator in terms of its generators. The boundary of any generator is a (p-1) chain. That is, for any generator c_i^p:
The integers a_ij^p form a matrix A^p, called the p-dimensional incidence matrix. The property δ^2 = 0 means that:
In matrix notation, this can be expressed as:
By suitable choice of generators of the groups G_p(K), all incidence matrices can be converted into diagonal matrices. This follows from the linear algebraic property that, for an integer matrix A, there are matrices M and N, such that the matrix MAN is of the form:
The sub-matrices in the top-left, top-right and bottom-right and all unmarked entire are zeros. An additional property of this matrix is that each d_i divides d_i+1 We transform each A^p to this form in turn.
Starting with A^1, we find matrices M^1 and N^1 such that:
The asterisks denoting its nonzero part. Let c^0 and c^1 be bases of first and second chain groups G_0(K) and G_1(K), respectively:
Replacing c^0 by (N^1)^-1c^0 and c^1 by M^1c^1, the boundary relations become:
The new one-dimensional incidence matrix is now D^1. Inductively, it follows that for each p, we find a new basis g^p, such that the boundary relations become:
where, g^p = [g_1^p; g_2^p; ...; g_k^p] and
This makes it convenient for us to split the column matrix g^p into a number of sub-columns, for each p:
The combined number of elements in α^p, β^p and γ^p is the number of zero rows in D^p. The number of elements in ρ^p is the number of units in D^p, and is equal to the number of elements in α^(p-1). The number of elements in ε^p is the number of non-zero non-unity elements in D^p. This is equal to number of t_i^p in D^p. It follows from the fact D^pD^(p-1) = 0, that the total number of elements in ρ^p and ε^p do not exceed the number of elements in α^(p-1), β^(p-1) and γ^(p-1). These boundary relations are summarised as:
Bases of the group G_p(K) with these properties are called standard bases or canonical bases. Let us recall the definition of pth homology group of a complex. It is the quotient group of p-cycles by p-boundaries. From the boundary relations above, we see the p-cycles group is generated by (α^p), (β^p), and (γ^p). All α_i^p are boundaries, while for each i, t_i^(p+1) β_i^p is a boundary. No linear combination of γ_i^p is a boundary. Following this, pth homology group is isomorphic to a direct sum of B_p and T_p. B_p is an additive group generated by γ_i^p and T_p is a direct sum of cyclic groups with orders t_1^(p+1), t_2^(p+1), ..., t_k^(p+1)
The number of γ_i^p in the canonical basis is called the pth betti number b_p of K. The order of T_p is called the pth torsion coefficient of K. Let n_p be the number of rows of incidence matrix A_p. This is equal to the number of generators of G_p(K). The pth betti number is also given by:
A popular theorem states:
where, the LHS is termed as Euler characteristic. For a chain complex with groups and homomorphisms,
The pth homology group H^p is denoted by quotient of kernels group Z^p by boundary group B^p:
Let me now try to mathematically formulate the algorithm synthesis problem.
Theory of Algorithm Synthesis
Various programs are categorised corresponding to the algorithms they implement. Similarly, various algorithms are categorised corresponding to the computable functions they implement. The collection of computable functions forms a quotient of collection of algorithms, which in turn form a quotient of programs. Viewing a program as an enumeration of instructions and data, we adopt the notion of 'algorithm is data'.
Algorithms, in algebraic topological terms, are cell complexes. The data and computational steps of an algorithm have incidence relations to them. Computational steps, or instructions, depend on (incident to) and produce (incident on) other computational steps. Data, on the other hand, have no entities incident to them. Regarding these incidence relations as boundary relations, this cell complex produces a chain complex.
A representative unit of a sub-structure of the chain complex is a program; the collection of allowable data (input) and instruction elements forms a programming language. Just like how a geometric figure is sub-divided into various kinds of cells, there are many ways of choosing a programming language. The algorithm we are looking for must produce some elements of the chosen programming language. We call them output. The program is a representative of our desired algorithm.
The ordering of instructions in a program is governed by its boundary. Say if an instruction depends on an element. And that element is not a part of the input. Then the instruction must be preceded by another instruction that produces that element. This induces a partial ordering of the instructions. That is, instructions belonging to a program need not necessarily be linearly ordered.
Algorithms for sorting, searching, generating permutations, generating clusters, generating subsets, generating partitions, generating graphs and job scheduling, etc., list all the elements of a set of combinatorial objects. Also, algorithms themselves when seen as sets of inputs and instructions are combinatorial objects. Now let us assume a programming language is chosen. It means we choose what type of instructions will be allowed in our algorithm. For example, the language which is used to list the genetic distance between two DNA sequences has only instructions which either swap two terms or delete a term from either sequence. A program then exists that produces any element of the entire chosen programming language. Let's call this program mother program. It is evident that other programs requiring only partial lists of elements of the chosen programming language are derivatives of mother program. The inputs necessary for derivative programs are a subset of the inputs necessary for the mother program.
The programming language is a finite set. The mother program can produce all elements of the programming language except those provided as input in the first place. Any derivative program that is needed to produce a partial list of elements of the set, is obtained by leaving some elements off, until all the instructions which depend on them have been performed.
We characterise an algorithm as an isomorphism class of a finite set of programs. The isomorphism follows a predefined axiomatic structure. We say two programs are isomorphic when there is an axiomatic structure preserving one-to-one correspondence between them.
The programming language (viewed as data) has its input and output kinds are provided via finite sets. A hierarchy of levels for data can be set up. The first set C_1 is a set of inputs and outputs. The second (higher level) set C_2 is set of instructions. That is, C_2 lists the ways in which some elements of C_1 are derived from others. Similarly, C_3 is a set which lists ways in which some elements of C_2 are derived from others. This hierarchical setup continues up to qth ordered set C_q.
To draw an analogy to our hierarchical setup, consider a game of chess. At level 1, for example, we have the set of white and black squares and pieces. Players in this level make tactical moves requiring decisions about a particular piece and a particular square. At a higher level 2, we have players operating on sets of squares (diagonally, centrally, etc.), where sets of pieces are positionally played to affect sets of squares. At the third level, players operate on a set of sets of sets of squares (like the Queen-side squares) and pieces. This accounts for a higher order tactical play. A sense of incidence among these sets can be observed here. Each lower order set is a derivative of its immediate higher order set. And each hierarchical set is representative of a convex polytope, with each set of vertices called as simplexes. A set on level n has dimension n. In a comparable sense, the dimension of an instruction is higher than the dimension of the data on which it operates. For example, the dimension of a high-level language is 4. Assembly language has dimension 3; machine code has dimension 2; and the integer values have dimension 1.
To offer a geometrical view, consider sets of integers (additive group), covered by set of instructions of first order, which in turn are covered by set of instructions of second order, and so on. A polygon formed from a set of instructions with non-overlapping edges in a plane such that each vertex is shared between two instructions. And a polyhedron is formed from a set of polygons with its faces in 3D space such that each set of instructions is shared between two faces. Repeating this construction (gluing) in sufficiently high-dimensional space, we get various higher dimensional polytopes.
A zero-dimensional polytope is a null set; in 1 dimension is an integer; in 2 dimensions is an instruction, etc. An n-dimensional polytope with smallest number of vertices is an n-simplex. Since we are operating on a hierarchy of convex sets, we have the property that for any two elements in the set, their connection also is a member of that set. It then follows that in a set of simplices, every face of any simplex in the set is also present in that set; and the intersection of any two simplices in the set is a face of both simplices. This set is called a simplicial complex. These simplices, if glued, are joined exactly at vertices, edges, triangular faces, and so on, without intersecting each other. Since each set is a derivative of its higher order set, we have a continuous function with a continuous inverse that exists between these two sets. We then say these two are homomorphic. Every positive-dimensional polytope can be represented as a simplicial complex, without introducing any new set elements.
The ordering of vertices {v_0,v_1,...,v_q} of a simplex defines an oriented q-simplex which we will denote and we say that a simplicial complex is oriented if all its simplices in are oriented. Recalling the definition of chain complex from earlier, let C_q (for each q ≥ 0) be the vector space whose bases is the set of all q-simplices of the oriented simplicial complex, and the elements are the linear combinations of basis vectors, called chains. Accordingly, C_q is called a chain group. The dimension of C_q is equal to the number of q-dimensional simplices of the simplicial complex. For q larger than the dimension of the simplicial complex, vector space C_q is trivial and equals to 0. For a set of vector spaces C_q the linear transformation δ_q:C_q → C_(q-1) called boundary operator acts on the basis vectors {v_0,v_1,...,v_q} in the standard way. Taking a sequence of chain groups C_q connected through the boundary operators δ_q we obtain a chain complex. The rank of the qth homology group is called q-dimensional holes in simplicial complex. The value of β_0 is the number of connected components of simplicial complex, β_1 is the number of tunnels, β_2 is the number of voids, etc. Each boundary operator δ_q has its matrix representation with respect to bases of vector spaces C_q and C_(q-1), with rows associated with the number of (q − 1)-simplices and the columns associated with the number of q-simplices.
We now have the programming language C:
generating a chain complex:
Which has many mother programs. Each mother program that generates all elements of the programming language corresponds to a canonical basis of the chain complex. Note that since we are operating on an integral domain (additive groups), we have chain complex same as the simplicial complex discussed earlier. Any two mother programs that generate the elements of language embedded in this chain complex on isomorphic. Intuitively, we can find the input set of the mother program by calculating a basis of the homology group of the chain complex.
Consider for example the pair of sets C_1 and C_2 that suggests a program. Note that this program is a part of the mother program. C_1 is a set consisting of the first-order elements of the program. That is, C_1 contains input elements and the elements obtained by applying instructions over input elements (result elements). C_2 is a set consisting of the second-order elements. That is, C_2 contains instructions that operate on elements of C_1, elements produced by third-order elements of C_3 and elements input to third-order elements of C_3. This hierarchal setup continues up to qth ordered set C_q.
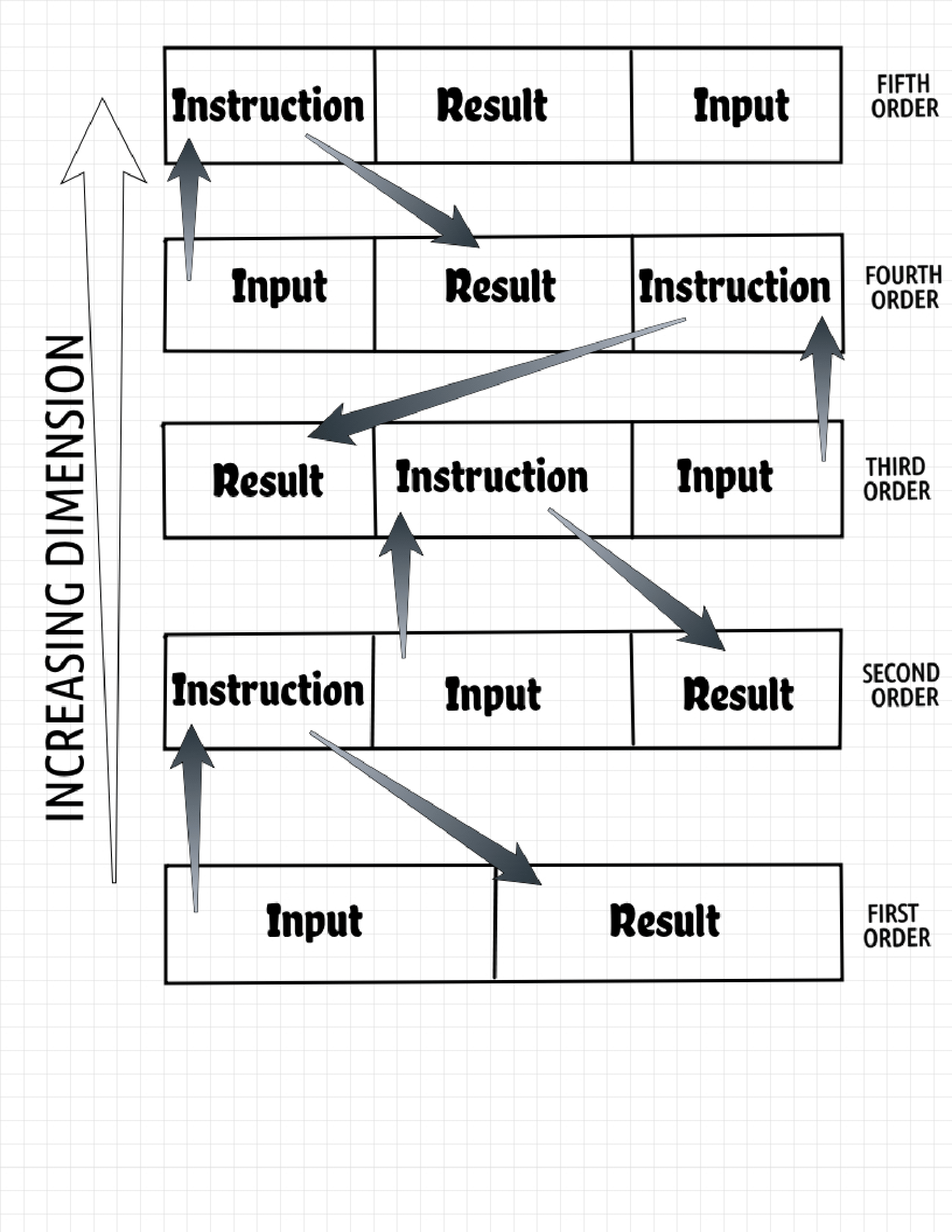
Any non-expanding formulation of this (co)chain would yield us both input and instructions by computing a basis. This basis however, is algebraic and we need to transform into a computational form. Few interesting off-shoots to peruse for later: the topology of algorithms, the geometry of machine code, and composability & equivalence of two algorithms.